Si vous êtes un propriétaire de terrain et que vous souhaitez savoir comment calculer la superficie d’un terrain, vous êtes au bon endroit.

Que votre terrain soit carré, rectangulaire ou de forme irrégulière, nous vous expliquons les méthodes simples pour mesurer la surface d’un terrain.

Multipliez la longueur de la base, b, par la hauteur, h, pour trouver l’aire totale. L’équation de l’aire, A, d’un carré ou d’un rectangle peut s’écrire comme suit : A = b * h. Dans notre exemple, la base, b, est de 12 pouces, et la hauteur, h, est de 5 pouces. Par conséquent, l’aire est de 12 pouces multipliés par 5 pouces, soit 60 pouces carrés.

Calcul de la Surface d’un Terrain Carré ou Rectangulaire

Parcelles ou terrains triangulaires

Ces types de terrains sont rarement trouvés, mais cela ne signifie pas que vous ne serez pas confrontés à ce problème.

Vous pouvez probablement trouver ces types de terrains au coin d’une route ou à un tournant.

Environ 85% des transactions immobilières impliquant des terrains nécessitent l’intervention d’un géomètre pour assurer la précision des mesures

Voici l’avi de Claire P, une géomètre expert :

« En tant qu’agent immobilier, il est essentiel pour moi d’avoir des mesures précises des terrains que je vends. J’utilise régulièrement des outils en ligne pour obtenir une estimation rapide avant de faire appel à un géomètre pour les mesures finales. »

Question : Calculez la surface d’un terrain triangulaire donné ayant respectivement 21 m, 13 m et 20 m de côté.

Solution :

Soit, le côté donné du triangle est,

(AB) = (a) = 21 mètres

(AC) = (b) = 21 mètres

(AB) = (c) = 21 mètres

Nous avons,

Aire du triangle (A) = racine carrée de s(s-a)(s-b)(s-c)
d’où s= demi-périmètre
a = longueur du 1er côté
b = longueur du 2ème côté
c = longueur du 3ème côté

On calcule donc d’abord les semi-périmètres (s) = (a+b+c)/2 = (20+21+13)/2 = 27 m.

Le semi-périmètre du triangle est la moitié de son périmètre, c’est-à-dire la somme de ses côtés.

Maintenant, en utilisant la formule ci-dessus, nous obtenons,

Aire du terrain triangulaire (A)

Ainsi, nous pouvons calculer la superficie des terrains de forme triangulaire.

Calculons maintenant la superficie des terrains rectangulaires.

Parcelles ou terrains rectangulaires

On trouve souvent ce type de terrain dans toutes les régions.

Les terrains dont un côté est égal à leur côté opposé et un autre côté est égal à un autre côté sont connus sous le nom de terrains rectangulaires.

Tous ses côtés sont perpendiculaires les uns aux autres, c’est-à-dire à 90 degrés.

Comprenons à l’aide des chiffres et de la figure ci-dessous.

Question : Calculez la surface d’un terrain rectangulaire dont les dimensions sont données dans la figure ci-dessous.

Solution : Ici, dans la figure, deux côtés sont de 14 mètres et deux autres de 8 mètres.

Ainsi, la longueur (L) = 14 mètres et la largeur (B) = 8 mètres.

Nous avons,

Surface du rectangle (A) = l X b

d’où l= longueur du côté

b= largeur du côté

Donc, en utilisant la formule ci-dessus, on obtient,
Superficie = l X b = (14 X 8) = 112 m2

De cette façon, nous pouvons calculer la superficie des terrains de forme rectangulaire.

Calculons maintenant la superficie des terrains carrés.

Parcelles ou terrains carrés

Ces types de terrains sont également courants dans toutes les régions.

Vous obtiendrez la forme du terrain le plus souvent et presque en forme rectangulaire ou carrée.

Les terrains dont tous les côtés sont égaux les uns aux autres sont connus sous le nom de terrains carrés.

Tous ses côtés sont perpendiculaires les uns aux autres, c’est-à-dire à 90 degrés.

Comprenons à l’aide de chiffres et de figures donnés ci-dessous.

Question : Calculez l’aire d’un terrain carré dont les dimensions sont données dans la figure ci-dessous.

Solution, Ici, dans la figure, tous les côtés sont égaux et font 8 mètres.

Donc, la longueur (L) = 8 mètres.

Nous avons,

Aire du carré (A)= l²
d’où l= longueur des côtés

En utilisant la formule ci-dessus,

Surface du terrain (A) = (8 X 8 ) m2 = 64 m2 ( mètres carrés)

Ainsi, nous pouvons calculer la superficie d’un terrain de forme carrée.

Calculons maintenant la superficie d’un terrain en forme de trapèze.

Terrain en forme de trapèze

Ce type de terrain peut être régulier ou irrégulier.

Nous allons décrire ici tous les types de terrain avec des exemples.

Discutons de tous les terrains à l’aide de chiffres et de formules pour les calculer.

A) Terrain ayant deux côtés parallèles l’un à l’autre

Ce type de terrain se trouve sur le bord de la route et peut être créé artificiellement dans un but différent.

Dans ce type de terrain, deux côtés sont parallèles l’un à l’autre mais les deux autres ne le sont pas.

Comprenons par un exemple.

Aire du trapèze (A) = 1/2 h (a+b)
d’où h= hauteur du trapèze
a= longueur supérieure du trapèze
b= longueur inférieure du trapèze

Vous pouvez également calculer la superficie du terrain ci-dessus en divisant le terrain en deux parties, un rectangle et un triangle, que vous pouvez voir sur la figure par la ligne verte.

Après cela, vous pouvez à nouveau utiliser la formule du carré et du triangle l’un par rapport à l’autre et obtenir la superficie totale.

Nous espérons que vous avez compris et que vous pouvez calculer la superficie de ces types de terrain.

Voyons un autre type de terrain irrégulier que vous avez généralement trouvé lors de l’enquête.

Mais ne vous inquiétez pas, nous allons également faire le calcul de ce terrain.

B) Terrain n’ayant aucun côté parallèle l’un à l’autre.

On trouve ce type de terrain partout dans les pays. Il s’agit de terrains irréguliers.

Dans ce type de terrain, tous les côtés sont différents les uns des autres et forment des angles différents les uns des autres.

Les géomètres doivent calculer ces types de terrains très souvent et ils rencontrent plus de problèmes pour calculer la surface réelle de ces terrains.

Le coût moyen d’un géomètre pour mesurer un terrain se situe entre 500 € et 2000 €

Comprenons avec des chiffres et des formules pour calculer la surface d’un terrain.

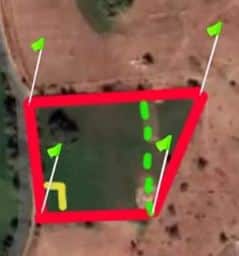
Question : Calculez la superficie d’un terrain irrégulier dont les dimensions sont indiquées dans la figure ci-dessous.

Solution :

Pour calculer ces types de terrain, c’est très facile.

Pour trouver la superficie de ces types de terrain, il faut d’abord enfouir quatre piquets ou des tiges de mesure à tous les coins du terrain.

Ensuite, il faut mesurer tous les côtés du terrain et garder à l’esprit que vous devez prendre la mesure de n’importe laquelle des diagonales.

Maintenant, vous pouvez voir dans la figure, le terrain total a été divisé en deux parties avec des diagonales de ligne bleue et ils sont en forme de triangles.

C’est tout, utilisez la formule des terrains triangulaires séparément et additionnez les deux pour obtenir la surface totale.

Passons maintenant au calcul,

Dans le triangle ABD,

Soit : BD (a) = 5 mètres, AD (b) = 3 mètres, AB (c) = 4 mètres.

Encore une fois, nous avons,

Aire du triangle (A) = racine carrée de s(s-a)(s-b)(s-c)
d’où s= demi-périmètre
a = longueur du 1er côté
b = longueur du 2ème côté
c = longueur du 3ème côté

d’où, S = (a+b+c)/2 = (5 + 3 + 4)/2 = 6 mètres.

Donc, en mettant toutes les valeurs, on obtient l’aire du triangle ABD,

= A1 = 6 m2

De la même façon, pour le triangle BDC,

Soit DC (a) = 13 mètres, BC (b) = 12 mètres, BD (c) = 5 mètres.

d’où, nous avons (S) = (a+b+c)/2 = (13 + 12 + 5)/2 = 15 mètres.

Donc, en mettant toutes les valeurs, on obtient l’aire du triangle BDC,

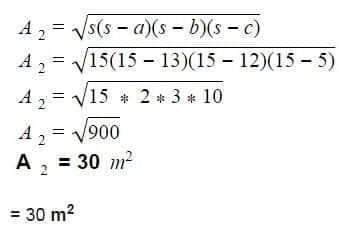
= 30 m2

Par conséquent, la superficie totale du terrain devient

= Aire du triangle ABD et du triangle BDC

= A1 + A2

= (6 + 30) m2

= 36 m2

Les calculateurs de surface en ligne peuvent estimer la superficie d’un terrain avec une précision de ±5%

J’espère que vous appréciez la lecture de cet article.

Vous ne savez pas trop combien votre investissement immobilier va vous rapporter en courte durée ?

Vous voulez savoir comment vous situer par rapport à la concurrence ?

Savez vous que 87% des millionnaires de l’immobilier louer en courte durée ont commencé par convaincre leur banquier grâce à une étude de marché ?

J’ai développé un outil qui utilise le Big Data pour réaliser pour vous une étude de marché parfaite.

Vous saurez exactement combien vous allez gagner, si l’investissement est rentable et comment vous démarquer de la concurrence :

Calculer la Superficie d’un Terrain

Bienvenue à notre quizz interactif sur le calcul de la superficie d’un terrain ! Testez vos connaissances et apprenez de nouvelles astuces pour mesurer précisément les différentes formes de terrain.

Instructions : Sélectionnez la réponse correcte pour chaque question. À la fin du quizz, vous recevrez un score et des explications pour chaque réponse.

Questions souvents posées par les lecteurs :

Qu’en pensez vous ?
Vous êtes libre de laisser un commentaire ci-dessous